Quantitative Models of Emergence in Light of Mathematical Theory of Human Systems
Part 2: Nonlinear Mathematical Models of New Quality Emergence
FEATURED PAPER
By Pavel Barseghyan, PhD
Texas and Armenia
Abstract
The second part of the article discusses the nonlinear functional relationships between system-level parameters of human systems underlying the deterministic emergence phenomenon.
The discussion is based on equations of state, which may be linear or nonlinear depending on the conditions of human activity.
Nonlinear relationships in equations of state are inherently divided into two categories.
The non-linearities of the first category are those contained in linear equations of state.
The second category of non-linearities is due to the limited capabilities of people and human systems, which are described by non-linear equations of state.
Introduction: The progress of human society occurs mainly in the nonlinear field of human activity
The requirements for mathematical models of any phenomenon or process are by their nature divided into two types: qualitative or behavioral requirements and quantitative requirements.
The first step towards mathematical modeling in terms of the quantitative description of the fundamental nature of phenomena and processes is to ensure qualitative or behavioral adequacy of the model.
By the behavioral adequacy of a mathematical model is meant a non contradictary reflection of the functional relationships between the characteristics of the object under study.
If the mathematical model is in a behavioral correspondence with the modeled phenomenon or process, then only after that one can proceed to ensure quantitative characteristics of the model.
The mathematical models considered in the first part of the article, which dealt with human activity and emergence phenomena, were qualitatively adequate only for linear cases, that is, when the duration of the actions or activities of people was directly proportional to their degree of complexity or difficulty [1, 2].
As a first approximation, this linear dependence can be obtained directly from the equation of state of an individual’s activity
![]()
This means that in the first part of the article, when developing a mathematical model of human activity and the emergence phenomenon, without mentioning it specifically, it is assumed that the above linear relationship is true for all levels of complexity or difficulty of human actions and activity.
The same is assumed in the case of a more detailed quantitative representation of the emergence phenomenon, which also takes into account human errors, in which the functional dependence T (D) has the following form [2].
![]()
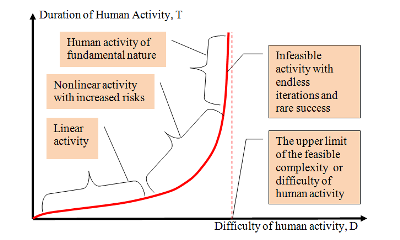
Fig.1. Functional relationship between human activity’s difficulty and duration (If the difficulty of human activity increases and approaches its upper limit, then its duration increases sharply because of endless iterations and gradually the activity of humans becomes infeasible)
As can be seen from expression (2), the dependence T (D) formally has a linear form, but a deeper examination of the issue shows that this expression contains a number of nonlinear dependencies that can only be revealed using additional extremе conditions that reflect the goals of people’s activities [ 3.4].
An analysis of the nonlinear relationships contained in the linear equation of state will be discussed below, and now we turn to the consideration of another important source of nonlinearity of the emergence phenomenon.
More…
To read entire article, click here
How to cite this paper: Barseghyan, P. (2020). Quantitative Models of Emergence in Light of Mathematical Theory of Human Systems – Part 2: Nonlinear Mathematical Models of New Quality Emergence; PM World Journal, Vol. IX, Issue IV, April. Available online at https://pmworldlibrary.net/wp-content/uploads/2020/03/pmwj92-Apr2020-Barseghyan-Quantitative-Models-of-Emergence-Part2-nonlinear-models.pdf
About the Author

Pavel Barseghyan, PhD
Yerevan, Armenia
Plano, Texas, USA
![]()
![]()
Dr. Pavel Barseghyan is a consultant in the field of quantitative project management, project data mining and organizational science. Has over 45 years’ experience in academia, the electronics industry, the EDA industry and Project Management Research and tools development. During the period of 1999-2010 he was the Vice President of Research for Numetrics Management Systems. Prior to joining Numetrics, Dr. Barseghyan worked as an R&D manager at Infinite Technology Corp. in Texas. He was also a founder and the president of an EDA start-up company, DAN Technologies, Ltd. that focused on high-level chip design planning and RTL structural floor planning technologies. Before joining ITC, Dr. Barseghyan was head of the Electronic Design and CAD department at the State Engineering University of Armenia, focusing on development of the Theory of Massively Interconnected Systems and its applications to electronic design. During the period of 1975-1990, he was also a member of the University Educational Policy Commission for Electronic Design and CAD Direction in the Higher Education Ministry of the former USSR. Earlier in his career he was a senior researcher in Yerevan Research and Development Institute of Mathematical Machines (Armenia). He is an author of nine monographs and textbooks and more than 100 scientific articles in the area of quantitative project management, mathematical theory of human work, electronic design and EDA methodologies, and tools development. More than 10 Ph.D. degrees have been awarded under his supervision. Dr. Barseghyan holds an MS in Electrical Engineering (1967) and Ph.D. (1972) and Doctor of Technical Sciences (1990) in Computer Engineering from Yerevan Polytechnic Institute (Armenia).
Pavel’s publications can be found here: http://www.scribd.com/pbarseghyan and here: http://pavelbarseghyan.wordpress.com/. Pavel can be contacted at terbpl@gmail.com









